AVL树、红黑树

BST树

BST树（二叉查找树）是一种特殊的二叉树，其左子节点的值小于父节点，右子节点的值大于父节点。

BST树特殊情况下会退化成一个链表，查询效率为线性。

AVL树

AVL树，平衡二叉树（一棵空树或者任意子树的高度差绝对值小于1的树），是一种特殊的BST树

下列一些示例介绍AVL树的平衡操作

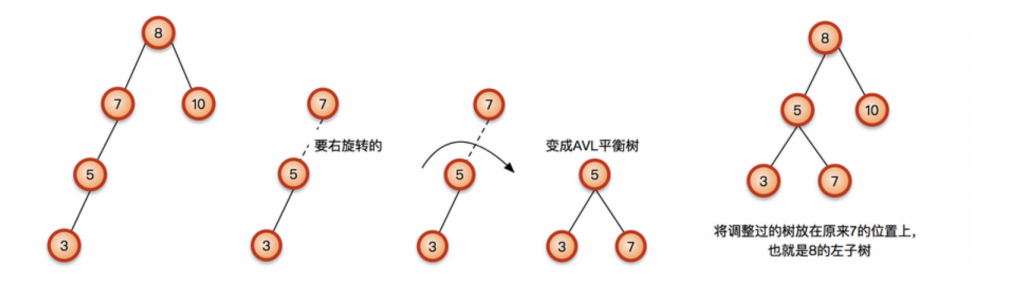
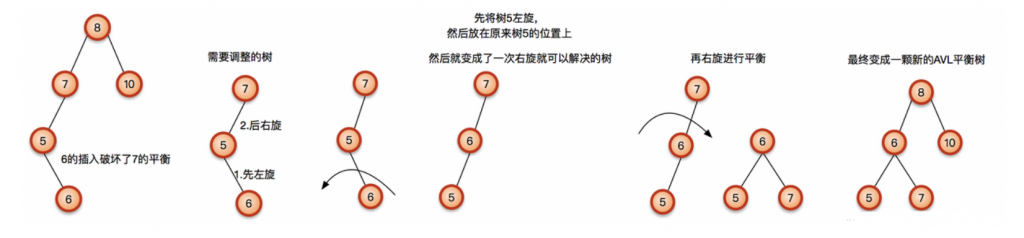
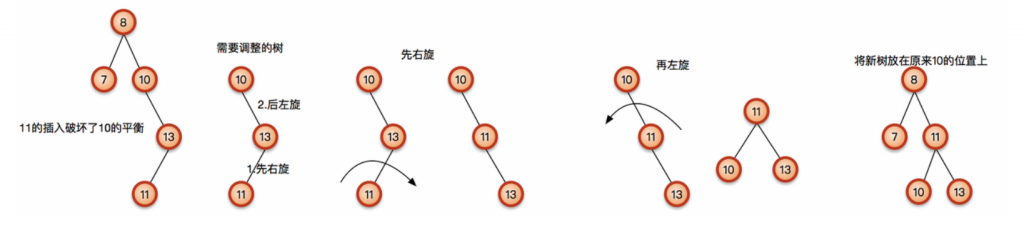
AVL树是高度平衡的，而为维持平衡，旋转操作较多，所以插入效率受到影响，查找效率较高。增加最多两次旋转O(1)，删除最多O(logn)，查找最多和平均都是O(logn)

红黑树

红黑树对于AVL树来说，是一种折衷的处理。

其中，增加最多两次旋转O(1)，删除最多3次旋转，查找最多和平均都是O(logn)

增加了一些定义，得到了一个综合效率更高的数据结构。

定义：

1.节点为黑色或者红色

2.根节点为黑色

3.叶子节点为黑色

4.红色节点的子节点必为黑色

5.根节点到叶子节点经过相同数量的黑色节点

由于这些特殊的定义，平衡性没有AVL树那么高，但是增加删除元素时消耗少。

红黑树的具体例子是java的treeMap

红黑树的旋转和变色，具体过程不在这里描述了。先挂个链接，是别人写的例子https://mp.weixin.qq.com/s/-8JFh5iLr88XA4AJ9mMf6g

下一篇会看一下B树和B+树，待续。。